Entrar/Criar Conta
Problemas de Lógica Matemática
Com certeza em algum momento da sua vida, seja na escola ou em uma situação cotidiana, você já deve ter se deparado com problemas de lógica matemática.
Esses desafios requerem que você utilize princípios e conceitos da lógica formal e da matemática para a resolução.
Normalmente, eles envolvem declarações ou proposições lógicas, regras de inferência, quantificadores, relações entre conjuntos e operações lógicas.
O objetivo é chegar a uma solução lógica que seja coerente e satisfaça as condições especificadas no problema.
Problemas de lógica matemática podem variar em complexidade, desde quebra-cabeças simples até problemas mais desafiadores que exigem um pensamento lógico rigoroso e uma abordagem sistemática.
Eles são frequentemente usados em competições matemáticas, testes de aptidão, testes de raciocínio lógico e em contextos acadêmicos para avaliar a capacidade das pessoas de aplicar a lógica e a matemática de forma eficaz.
Resolução de problemas de lógica matemática
A resolução de problemas lógicos em diferentes áreas envolve abordagens específicas com base nos conceitos e regras associados a cada uma dessas áreas.
Existem várias maneiras de resolver problemas de lógica matemática e, neste capítulo, vamos especificar algumas das principais delas.
Quebra-Cabeças Lógicos
Os quebra-cabeças lógicos são desafios ou enigmas que exigem raciocínio lógico, pensamento crítico e resolução de problemas para serem resolvidos.
Eles são projetados para entreter, educar e estimular o cérebro, geralmente apresentando situações complexas que precisam ser desvendadas seguindo regras lógicas ou padrões específicos.
Dentre os quebra cabeças lógicos, os mais conhecidos são:
Sudoku: O Sudoku é um quebra-cabeça numérico em que você preenche uma grade 9x9 com números de 1 a 9, seguindo regras específicas. Cada linha, coluna e sub grade 3x3 deve conter todos os números de 1 a 9 sem repetições.
Quebra-cabeça de lógica: Este tipo de quebra-cabeça apresenta uma situação com várias variáveis e regras, e você deve deduzir as soluções usando raciocínio dedutivo. Um exemplo é o quebra-cabeça de lógica com casas coloridas, onde você deduz a cor de cada casa com base em pistas dadas.
Quebra-cabeça de enigmas: Esses quebra-cabeças envolvem resolver enigmas escritos para chegar a uma resposta. Por exemplo, "Você tem uma galinha, uma raposa e uma sacola de milho. Você deve atravessar um rio em um barco que só pode transportar você e mais uma coisa de cada vez. Como você levará todos os itens para o outro lado do rio sem deixar a galinha sozinha com a raposa ou a raposa sozinha com o milho?"
Quebra-cabeças de padrões: Esses quebra-cabeças desafiam você a identificar padrões em sequências de números, letras ou figuras. Por exemplo, encontrar o próximo número em uma sequência de Fibonacci.
Quebra-cabeças de encaixe: Esses quebra-cabeças envolvem manipular peças físicas para encaixá-las em uma configuração específica. O Tangram é um exemplo clássico de um quebra-cabeça de encaixe.
Quebra-cabeças de palavras: Jogos de palavras como palavras cruzadas, charadas e criptogramas são exemplos de quebra-cabeças de palavras que desafiam seu conhecimento e habilidades de decodificação.
Quebra-cabeças matemáticos: Esses quebra-cabeças exigem a aplicação de conceitos matemáticos para resolver problemas. O quebra-cabeça do cavalo no tabuleiro de xadrez é um exemplo, onde você deve encontrar uma série de movimentos para o cavalo que o leva a todas as casas do tabuleiro sem repetições.
Lógica Proposicional
O tópico de lógica proposicional vimos anteriormente mas para recapitular neste estudo, esta área se concentra nas operações lógicas que podem ser aplicadas a proposições e como essas operações afetam a verdade ou falsidade das proposições compostas.
A lógica proposicional usa símbolos e conectivos lógicos para representar proposições e suas relações. Aqui estão alguns exemplos de proposições e conectivos lógicos:
Proposições Simples: São afirmações que podem ser verdadeiras ou falsas, como:
P: "O sol está brilhando."
Q: "Está chovendo."
R: "2 + 2 = 5."
Lógica de Primeira Ordem
A lógica de primeira ordem, também conhecida como lógica de predicados de primeira ordem ou lógica de ordem superior, é uma extensão da lógica proposicional.
Ela permite a representação de quantificadores, variáveis, funções e predicados, tornando-a mais expressiva e capaz de lidar com argumentos mais complexos e estruturados.
Por meio desse modelo lógico é possível descrever relações e propriedades em um nível mais profundo do que a lógica proposicional.
Nessa lógica, existem alguns dos principais conceitos que você deve conhecer:
Variáveis: Na lógica de primeira ordem, usamos variáveis para representar objetos ou elementos de um domínio específico. Exemplos de variáveis incluem x, y, z, etc.
Predicados: Os predicados são proposições que contêm variáveis e podem ser avaliados como verdadeiros ou falsos dependendo das substituições das variáveis. Por exemplo, P(x) pode ser um predicado que significa "x é um número par."
Quantificadores: A lógica de primeira ordem inclui quantificadores que indicam como uma proposição se aplica a variáveis. Os dois principais quantificadores são:
Quantificador Universal (∀): Representa "para todo" ou "para cada". Por exemplo, ∀x P(x) significa "para todo x, x é um número par."
Quantificador Existencial (∃): Representa "existe" ou "pelo menos um". Por exemplo, ∃x P(x) significa "existe pelo menos um x que é um número par."
Funções: Funções são usadas para mapear variáveis em outros objetos. Por exemplo, f(x) pode ser uma função que representa o sucessor de x.
Sentenças Quantificadas: Sentenças na lógica de primeira ordem frequentemente incluem quantificadores, variáveis e predicados. Um exemplo é a sentença ∀x (P(x) → Q(x)), que pode ser lida como "para todo x, se P(x) for verdadeiro, então Q(x) também é verdadeiro."
A lógica de primeira ordem pode ser utilizada da seguinte forma:
Considere o domínio de todos os números inteiros e os predicados:
P(x) "x é um número par"
Q(x) "x é um múltiplo de 4".
Podemos expressar a afirmação "todos os múltiplos de 4 são números pares" na lógica de primeira ordem da seguinte forma:
∀x (Q(x) → P(x)). Isso afirma que para todos os números x, se x é um múltiplo de 4, então x também é um número par.
Teoria dos Conjuntos
A teoria dos conjuntos é uma parte importante da matemática que se concentra na formalização e estudo de conjunt
Ela ajuda a estabelecer uma base sólida para a representação e manipulação de objetos e relações em contextos lógicos e matemáticos.
A teoria dos conjuntos desempenha um papel fundamental no raciocínio lógico, pois fornece uma estrutura sólida para organizar e manipular informações de uma maneira lógica e coerente.
Na lógica, as proposições são declarações que podem ser verdadeiras ou falsas. A teoria dos conjuntos permite que você defina conjuntos de elementos que representam as condições lógicas e as relações entre essas proposições.
Então, por exemplo, você pode criar um conjunto que representa todos os elementos que satisfazem uma determinada condição lógica.
Não somente, as operações de conjuntos, como união, interseção e complemento, são usadas para representar operações lógicas.
Uma interseção de dois conjuntos pode representar a conjunção de duas proposições (ambas devem ser verdadeiras para que a interseção seja não vazia), enquanto a união pode representar a disjunção (pelo menos uma deve ser verdadeira).
Ao representar informações e relações de maneira lógica e estruturada, a teoria dos conjuntos ajuda na resolução de problemas.
Problemas de Combinatória
Problemas de combinatória na lógica envolvem a contagem e a análise de arranjos, permutações, combinações e outras estruturas de conjuntos em contextos lógicos e matemáticos.
Esses problemas estão relacionados à teoria da combinatória, que lida com a contagem de maneiras diferentes de organizar, agrupar ou selecionar elementos de um conjunto finito.
A combinatória na lógica pode ser aplicada em várias áreas e, para você conhecer melhor, aqui vão alguns exemplos de problemas de combinatória na lógica:
Arranjos e Permutações: Problemas de arranjos e permutações na lógica envolvem organizar elementos em uma ordem específica.
Você saberia me dizer quantas permutações diferentes podem ser formadas usando as letras da palavra "LOGICA"?
Para calcular o número de permutações diferentes que podem ser formadas usando as letras da palavra "LOGICA", você pode usar a fórmula para permutações de um conjunto de elementos com repetições. Nesse caso, temos a letra "L" repetida duas vezes e a letra "A" repetida duas vezes.
A fórmula geral para permutações com repetições de um conjunto de n elementos, onde n1 elementos são do mesmo tipo, n2 elementos são de outro tipo, e assim por diante, é dada por:
- O sistema de segurança é ativado quando S2 e S3 estão ativos.
- Também é ativado quando S1 e S3 estão ativos.
- E é ativado quando S1 e S2 estão ativos.
Este artigo pertence ao Curso Raciocínio Lógico Básico
Curso GRÁTIS sem mensalidade, sem taxa de matrícula.COMENTÁRIOS
5.0
12.743 AvaliaçõesÓtimo curso, mesmo que já é coisas que faço no meu dia a dia foi bem bacana a experiência de fazer este curso super recomendo.
Maravilhoso
MARAVILHA. MUITO BOM.
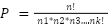
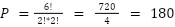
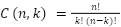
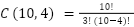
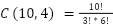
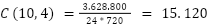
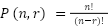
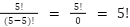
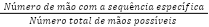
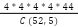
Parabéns! Muito bom, me sinto como realizando o serviço.
Ótimo curso, mesmo que já é coisas que faço no meu dia a dia foi bem bacana a experiência de fazer este curso super recomendo.
Muito bom
Maravilhoso
Muito bom
MARAVILHA. MUITO BOM.